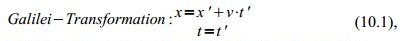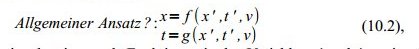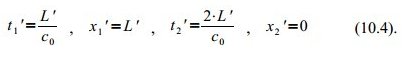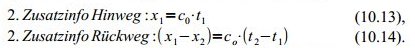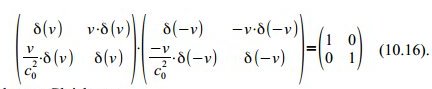….versucht die Relativitätstheorie zu verstehen“
Denn in jener Reihe bin ich von der Lorentz-Transformation einfach ausgegangen, ohne diese näher zu hinterfragen.
Das wollen wir diesmal tun.
Einleitung
Nachdem die Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“ auf diesem Blog schon einige Zeit her ist, müssen wir also wieder von vorne beginnen.
Wir erinnern uns, der Ausgangspunkt ist die Konstanz der Lichtgeschwindigkeit.
Wenn wir also einen ruhenden Beobachter haben, dann bewegt sich ein Lichtblitz im leeren Raum relativ zu diesem Beobachter mit der Geschwindigkeit c0 = 2,998.108 m/sec (also etwa 300.000 km/sec).
Wenn sich nun ein anderer Beobachter und seine Meßgeräte mit der Geschwindigkeit v bewegen (v < c0 ), dann bewegt sich der Lichtblitz relativ zu diesem bewegten Beobachter nicht mit der Geschwindigkeit c0 minus v, wie man intuitiv vermuten könnte, sondern eben auch mit der Geschwindigkeit c0. Das ist experimentell bestätigt.
Beide Beobachter beobachten natürlich denselben Lichtblitz. Wir wollen ausschließen, dass durch die Bewegung des einen Beobachters die Wirklichkeit in zwei Wirklichkeiten „zerbricht“, und man dadurch zwei unterschiedliche Lichtblitze bekommt.
Wenn es nun aber immer derselbe Lichtblitz ist, und wenn er sich relativ zum ruhenden und zum bewegten Beobachter immer mit derselben Geschwindigkeit bewegt, dann kann irgendetwas mit Raum und Zeit nicht mehr stimmen, da ja derselbe Lichtblitz relativ zu beiden Beobachtern „gleichzeitig“ unterschiedliche Weglängen zurücklegen müßte und das mit derselben Geschwindigkeit.
Auf den ersten Blick ist das eine immense Widersprüchlichkeit, zumindest für unsere Intuition.
Der Verdacht liegt nahe, dass sich Raum und/oder Zeit für einen bewegten Beobachter in irgendeiner Weise deformieren. Insbesondere hegen wir den Verdacht, dass die sogenannte Galilei-Transformation nicht mehr gilt.
Zu allem Überdruss kommt noch das Relativitätsprinzip hinzu, das uns sagt, dass es gar nicht absolut feststellbar ist, welcher der beiden Beobachter sich bewegt und welcher stillsteht, man kann nur sagen, dass sie sich relativ zueinander mit einer Geschwindigkeit v bewegen.
Wenn man etwas nicht versteht, oder wenn man etwas von vorne weg nochmal analysieren möchte, dann ist es oft hilfreich mit einem einfachen Beispiel und einer Zeichnung zu beginnen.
Modellbildung
Beginnen wir also mit einem einfachen Beispiel. Am besten, wir ignorieren vorerst die Gravitation (die wird erst in der allgemeinen Relativitätstheorie erklärt) und verlegen das Beispiel in den Weltraum.
Eine Raumstation fernab von allen Planeten und Sternen sei unser „ruhendes“ Bezugssystem. Jahrzehntelang gibt es in einem weiten Umkreis um diese Raumstation einfach nichts ausser dem leeren Raum und auch etwaige Antriebsraketen der Station sind deaktiviert.
Eines Tages geschieht es nun, dass ein Raumschiff an der Station vorbeifliegt, und zwar mit hoher aber konstanter Geschwindigkeit v (auch die Antriebsraketen des Raumschiffs sind ausgeschaltet).
Im Raumschiff wird gerade ein wissenschaftliches Experiment durchgeführt. Und zwar wird ein Lichtblitz vom hinteren Ende des Raumschiffs durch eine Vakuumröhre zum vorderen Ende gesendet und dort an einem Spiegel reflektiert. Die Laufzeit des Lichtblitzes wird gemessen, und zwar für den Hinweg und für den Rückweg.

Geht es auch ohne Mathematik?
Wenn wir uns dieses Beispiel ein wenig näher anschauen, dann wird unsere Intuition und unser Intellekt auf eine harte Probe gestellt.
Denn die Behauptung ist, dass die Lichtgeschwindigkeit konstant ist und dass es sich trotzdem immer um denselben Lichtblitz handelt, ganz egal, welcher Beobachter ihn mißt.
Wir wollen nun den Weg des Lichtblitzes verfolgen, und zwar zweimal, einmal aus der Sicht des ruhenden Beobachters und einmal aus der Sicht des bewegten.

Einmal sind beide Wege, der Hinweg und der Rückweg gleich lang, beim anderen Mal ist der Hinweg länger als der Rückweg.
Wenn nun das Licht immer gleich schnell ist, dann kommen wir in Bedrängnis mit unserem Begriff der Gleichzeitigkeit, denn im bewegten System vergeht für Hin-und Rückweg sicherlich dieselbe Zeit, während im ruhenden System der Hinweg länger dauert als der Rückweg.
Die Uhren im bewegten System gehen offensichtlich anders als die Uhren im ruhenden System, und offensichtlich ist das Ganze auch noch vom Wert der x-Koordinate abhängig. Der Begriff einer absoluten Zeit, die in allen Bezugssystemen gleich schnell verläuft (t=t‘), ist also mit Sicherheit zu verwerfen.
Allein mit unserer Intuition kommen wir hier nicht weiter. Wir werden also reumütig die ach-so-verhaßte Mathematik bitten, uns wieder einmal zu helfen.
Mathematische Analyse
Wir versuchen nun das wissenschaftliche Experiment, welches in jenem Raumschiff durchgeführt wird, mathematisch zu beschreiben.
Dazu nehmen wir die drei wichtigsten Ereignisse des Experiments und benennen ihre Orts- und Zeitkoordinaten.
Da wir ja den Verdacht hegen, dass sich Raum und Zeit für einen bewegten Beobachter verzerren, müssen wir jedes Ereignis vorläufig durch 4 Zahlen beschreiben: Orts- und Zeitkoordinate im bewegten System (wir nennen es das „gestrichene“ System, obwohl das Raumschiff wahrscheinlich metallisch blank ist 🙂 ) sowie Orts- und Zeitkoordinate im unbewegten System (wir nennen es das „ungestrichene“ System).
- Ereignis E0: Lichtblitz wird ausgesendet: x0, t0, x0‚, t0‚
- Ereignis E1: Lichtblitz wird reflektiert: x1, t1, x1‚, t1‚
- Ereignis E2: Lichtblitz trifft wieder ein: x2, t2, x2‚, t2‚
Diese 12 Werte wollen wir nun herausfinden. Bei einigen wird das leicht sein, bei anderen ein wenig schwieriger.
Letzten Endes wollen wir natürlich den Zusammenhang zwischen den ungestrichenen Werten und ihren gestrichenen Companions ganz allgemein herausfinden.
Wir haben den Verdacht, dass wir diesen Zusammenhang nicht mehr durch die Galilei-Transformation beschreiben können,also nicht:
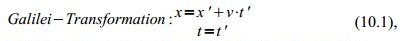
sondern dass der Vektor (x,t) in allgemeinerer Form vom Vektor (x‘,t‘) abhängt.
Ziemlich allgemein könnte man schreiben
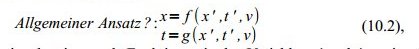
wobei f() und g() zwei zu bestimmende Funktionen in den Variablen x‘ und t‘ sowie mit dem (konstanten) Parameter v wären.
Nun, solch allgemeine Ansätze wollen wir getrost der allgemeinen Relativitätstheorie überlassen, vorerst betreiben wir spezielle Relativitätstheorie und begnügen uns mit einem speziellen, nämlich mit einem linearen Ansatz (später wird sich zeigen, dass dieser lineare Ansatz für kleine Gebiete der Raumzeit näherungsweise in der allgemeinen Relativitätstheorie immer noch gilt).
Wir stellen die Transformation des Vektors (x‘,t‘) in den Vektor (x,t) also durch eine Lineartransformation dar:

Wir nehmen also das Ziel ins Visier, die Koeffizienten α, β, γ und δ ganz allgemein zu berechnen.
Na gut, wer nicht anfängt, wird auch nicht fertig. Also „los!“
Da es physikalisch unerheblich ist, wo der Nullpunkt der Bezugssysteme liegt, legen wir den Nullpunkt der x-Achse willkürlich an den Punkt, an dem das Raumschiff die Raumstation passiert und an dem das Ereignis E0 stattfindet (x0 = 0).
Die Ortskoordinate im Raumschiff messen wir willkürlich „vom hinteren Ende nach vorne“ (x0‚ = x2‚ = 0) und wir legen den Zeitnullpunkt in das Ereignis E0 (t0 = t0‚ = 0).
Weiters nehmen wir an, dass wir die Länge des Raumschiffes kennen (L‘ sei gegeben, also x1‚ = L‘). Allerdings müssen wir hier vorsichtig sein. Da wir ja vermuten, dass sich Raum und Zeit durch die Bewegung verzerren, müssen wir davon ausgehen, dass der ruhende Beobachter eine andere Länge L mißt als der mitbewegte Beobachter (der mißt L‘).
Da wir die Länge L‘ des Raumschiffes und die Geschwindigkeit des Lichtblitzes c0 kennen, können wir alle gestrichenen Größen leicht berechnen:
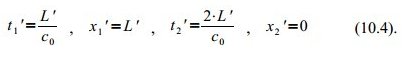
Fassen wir also noch einmal zusammen, was wir bereits wissen:

Wir können also bereits einige Gleichungen aufstellen, um unsere Koeffizienten α, β, γ und δ zu berechnen:
Die Transformationsgleichungen für das Ereignis E0 liefern leider keinen verwertbaren Beitrag:

also die Werte eingesetzt:

Diese Gleichung liefert keine Aussage über unsere Koeffizienten, da sie für beliebige Koeffizienten immer gültig ist (0=0).
Das ist eben ein Ausdruck der Tatsache, dass wir die Lage der Ursprünge der Bezugssysteme selbst und willkürlich festgelegt haben und jetzt aufgrund dieser Lage keine neue Aussage erwarten können.
Von den beiden anderen Ereignissen können wir uns mehr erwarten.


Wir haben jetzt also 4 Gleichungen – (10.7) und (10.8) – sowie 8 Unbekannte (die Ereignisse E1 und E2 aus der Sicht des unbewegten Beobachters (x1, t1, x2 und t2) sowie die Koeffizienten α, β, γ und δ).
Wir müssen also nach weiteren Informationen suchen.
Suche nach weiteren Informationen
Zuallererst verwerten wir die Information, dass sich das Raumschiff ja mit der Geschwindigkeit v bewegt. Dies äußert sich in folgender Gleichung:

Wenn wir die Gleichungen (10.8) und (10.9) kombinieren, dann bekommen wir bereits eine Aussage über die Koeffizienten β und δ:

Damit kann man den Koeffizienten β in den Gleichungen (10.7) und (10.8) eliminieren:


Jetzt denken wir wieder an unseren Ausgangspunkt, dass sich der Lichtblitz nämlich auch relativ zum unbewegten System mit der Geschwindigkeit c0 bewegt. Damit können wir zwei Gleichungen aufstellen, eine für den Hinweg und eine für den Rückweg:
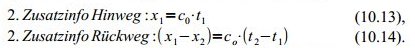
Die beiden Gleichungen (10.13) und (10.14) kann man ein wenig umschreiben, um dann die Werte x1, x2, t1 und t2 in (10.11) und (10.12) zu eliminieren.
Das ist jetzt ein wenig Rechenarbeit, aber zum Schluß wird auch der werte Leser folgende Zusammenhänge zwischen den Koeffizienten α, β, γ und δ feststellen:

Mit (10.15) haben wir jetzt drei Gleichungen, um die vier Koeffizienten festzulegen, wobei die konkreten Ereignisse (x1, t1, x2, t2) bereits eliminiert sind.
Ein bisschen Information fehlt aber noch.
So denken wir jetzt an das Relativitätsprinzip, welches uns sagt, dass keines der beiden Bezugssysteme bevorzugt sein darf.
Wenn also die Raumstation statt dem Raumschiff das wissenschaftliche Experiment durchführen würde, dann wären die Ergebnisse genau dieselben, man müßte bloß v durch minus v ersetzen (da sich die Raumstation relativ zum Raumschiff mit der Geschwindigkeit -v bewegt) und die gestrichenen Werte mit den ungestrichenen vertauschen.
Mathematisch läßt sich das elegant mit Hilfe der Matrizenrechnung formulieren. Wir sagen: wenn man die Matrix der Hintransformation mit der Matrix der Rücktransformation multipliziert, muss dabei die Einheitsmatrix herauskommen (das ist so ähnlich wie x.(1/x)=1).
Also alle Koeffizienten durch δ(v) ausdrücken (siehe (10.15)) und beide Transformationsmatrizen multiplizieren:
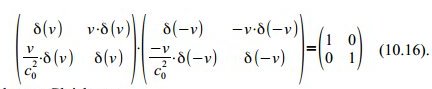
Das führt letzten Endes zur Gleichung

und zu den bekannten Gleichungen der Lorentz-Transformation:

Fazit
Wir haben jetzt also nichts anderes gemacht, als die Lorentztransformation aus folgenden Tatsachen herzuleiten:
- Konstanz der Lichtgeschwindigkeit
- Es soll sich um eine Lineartransformation handeln
- Relativitätsprinzip
was man übrigens in jedem Lehrbuch der Physik trefflich nachlesen kann.
Ich war Euch das einfach schuldig, liebe Leser, da ich in der Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“ die Lorentz-Transformation stets als gegeben akzeptiert hatte und mich nur mit den Konsequenzen beschäftigte.
Links
Die Links zu den anderen Artikeln der Serie findet Ihr hier: Zurück an den Start!
Gute Artikel zur Relativität findet man auf „Einstein Online“ (http://www.einstein-online.info/)



 Veröffentlicht von Yeti
Veröffentlicht von Yeti