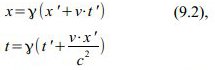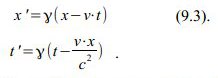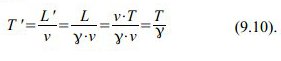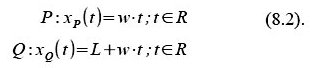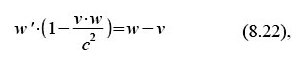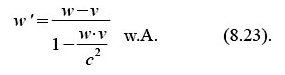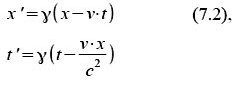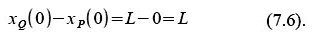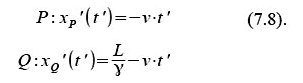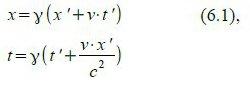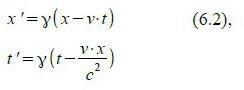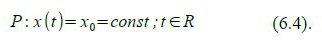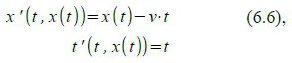Christophs Blog

Willkommen zu einem frischen Artikel in der Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“.

Hier wird versucht, anhand einiger einfacher Beispiele den Ideen der Relativitätsheorie auf die Schliche zu kommen.

Im ersten Artikel dieses Fünfer-Blocks (siehe „Zurück an den Start“) hatten wir die LT (Lorentz-Transformation) für Ereignisse angeschrieben. Dabei hatten wir akzeptiert, dass Zeit keine absolute (invariante) Größe ist.

Beim letzten Mal (siehe „Länge ist relativ“) haben wir gesehen, dass auch Längen keine absoluten Größen darstellen, sondern ebenfalls vom Bewegungszustand des Beobachters abhängen.

Na gut, da ja eine Geschwindigkeit sich aus „Länge pro Zeit“ ergibt, ist es naheliegend, dass sich bei der Transformation von Geschwindigkeiten ebenfalls etwas ändern wird, wenn man relativistisch an die Sache herangeht.

Wir definieren also wieder ein ungestrichenes („ruhendes“) Bezugssystem und ein gestrichenes („bewegtes“) Bezugssystem, der Stab bewege sich diesmal aber relativ zu beiden Bezugssystemen.

Genauer definieren wir:

• Das gestrichene Bezugssystem bewege sich wieder relativ zum ungestrichenen mit der konstanten Geschwindigkeit v.
• Der Stab bewege sich relativ zum ungestrichenen Bezugssystem mit der Geschwindigkeit w≠v.

Wir beginnen wieder mit der – Newton’schen – Zeichnung der Situation, wohl wissend, dass wir dadurch unser Gehirn auf falsche Bahnen lenken könnten, aber in der Hoffnung, die Sache anschaulicher zu gestalten.

Vorerst wollen wir die Ergebnisse, die wir bereits gesammelt haben, nützen, um unsere Erwartungen zu formulieren.

Dazu führen wir ein drittes, zweigestrichenes, Bezugssystem ein, welches sich mit dem Stab mitbewegt.

Wir wissen, dass sich das gestrichene Bezugssystem mit der Geschwindigkeit v relativ zum ungestrichenen bewegt, auch wissen wir, dass sich der Stab mit Geschwindigkeit w relativ zum ungestrichenen bewegt, aber – was uns zur Beantwortung der Frage führen soll – bewegt sich der Stab relativ zum gestrichenen Bezugssystem tatsächlich mit der Geschwindigkeit w’=w–v, wie wir aufgrund der Newton’schen Mechanik erwarten würden?

Um das zu erforschen, transformieren wir wieder die Weltlinien der beiden Endpunkte des Stabes. Diese Punkte P und Q bewegen sich dabei mit der Geschwindigkeit w relativ zum „ruhenden“ Bezugssystem:

Nun gut, um die Weltlinien der Punkte P und Q zu transformieren, verwenden wir wieder die Lorentz-Transformation

und setzen die Weltlinie des Punktes Q ein (Q ist der allgemeinere Fall, P folgt aus Q durch das Setzen von L gleich 0):

Die zweite Gleichung in die erste eingesetzt, und nach x‘ aufgelöst, ergibt in weiterer Folge x'(t‘).

Zuerst eingesetzt

dann alle Summanden mit x‘ auf die linke Seite gebracht

vereinfacht mit

zu

und weiter

also konkret für die beiden Weltlinien

Wir sehen also, dass sich die Geschwindigkeiten der Bezugssysteme NICHT einfach subtrahieren, wie in der Newton’schen Mechanik, sondern dass sich die Relativgeschwindigkeit der beiden Bezugssysteme, die sich mit v bzw. w bewegen, wie folgt ergibt (Geschwindigkeit des zweigestrichenen Systems aus der Sicht des gestrichenen Systems (v)):

Das ist auch einleuchtend: angenommen, ein Stab bewege sich (fast) mit Lichtgeschwindigkeit nach rechts, ein anderer (fast) mit Lichtgeschwindigkeit nach links, dann können sich die beiden Stäbe relativ zueinander nicht mit doppelter Lichtgeschwindigkeit bewegen.

Da sowohl w als auch v betragsmäßig immer kleiner oder gleich der Lichtgeschwindigkeit sein müssen, ist der „Korrekturfaktor“ immer im Bereich zwischen 0 und 2. Wenn w und v dasselbe Vorzeichen haben (wenn sich die Bezugssysteme in dieselbe Richtung bewegen), dann ist der Faktor kleiner 1, die „relativistische Relativgeschwindigkeit“ ist also größer als die „Newton’sche Relativgeschwindigkeit“. Wenn die Geschwindigkeiten unterschiedliches Vorzeichen haben, dann ist der Faktor größer 1, die „relativistische Relativgeschwindigkeit“ ist also kleiner als die Newton’sche.

Jetzt könnte man sich eine Zwischenfrage stellen.

Denn so einleuchtend der Zusammenhang

auch ist, so unsymmetrisch scheint dieses Ergebnis zu sein.

Oder – anders formuliert – wären wir zum selben Ergebnis gekommen, wenn wir entweder das gestrichene oder das zweigestrichene Bezugssystem als „ruhendes“ angesetzt hätten und sodann die Relativgeschwindigkeit der anderen beiden berechnet hätten?

Um diese Fragestellung zu beleuchten, überlegen wir uns einmal, welche Fälle es gibt. Dazu machen wir eine Zeichung der Bezugssysteme B, B‘ und B“ sowie ihrer Relativgeschwindigkeiten:

Wenn wir drei Bezugssysteme haben, dann kann sich also jedes der drei Bezugssysteme relativ zu jedem mit einer bestimmten Geschwindigkeit bewegen, im ersten Ansatz haben wir also 9 Relativgeschwindigkeiten und damit 9 Freiheitsgrade:

u…………………Geschwindigkeit von B, relativ zu B
u’………………..Geschwindigkeit von B, relativ zu B‘
u“……………….Geschwindigkeit von B, relativ zu B“
v…………………Geschwindigkeit von B‘, relativ zu B
v’………………..Geschwindigkeit von B‘, relativ zu B‘
v“……………….Geschwindigkeit von B‘, relativ zu B“
w………………..Geschwindigkeit von B“, relativ zu B
w’……………….Geschwindigkeit von B“, relativ zu B‘
w“………………Geschwindigkeit von B“, relativ zu B“

Da man aber aus physikalischer Vernunft und aufgrund der Ergebnisse des zweiten Artikels (siehe „Manchmal sind offensichtliche Dinge gar nicht so offensichtlich“) bereits einige Gleichungen aufstellen kann, nämlich

• ein Bezugssystem bewegt sich relativ zu sich selbst immer mit der Geschwindigkeit 0 und
• wenn sich Bezugssystem B1 relativ zu B2 mit der Geschwindigkeit v bewegt, dann bewegt sich B2 relativ zu B1 mit der Geschwindigkeit -v,

so bleiben 3 Freiheitsgrade.

Weiters haben wir die Beziehung zwischen w‘, v und w bereits hergeleitet, nämlich

Diese Gleichung bezieht sich auf das linke Dreieck in Abbildung (8.12).

sodass eben nur mehr zwei Freiheitsgrade offen sind. Damit müssen wir jetzt also beweisen, dass unter all diesen Voraussetzungen die folgenden beiden Annahmen wahr sind:

diese Gleichung bezieht sich auf das mittlere Dreieck in Abbildung (8.12), und

diese Gleichung bezieht sich auf das rechte Dreieck in Abbildung (8.12).

Diese Annahmen ergeben sich, indem man für die bereits hergeleitete Formel w‘ = w'(w,v) den „Sichtwinkel ändert“ und die Relativgeschwindigkeiten aus Sicht der beiden anderen Fälle einsetzt (reiner Analogieschluß).

Beweis für Annahme 1:

Die Beziehung u’=-v in Annahme 1 eingesetzt

sodann aufgelöst nach w‘ mit

und

ergibt den Beweis:

Beweis für Annahme 2:

Die Beziehungen u“=-w und w’=-v“ in Annahme 2 eingesetzt

sodann aufgelöst nach w‘ mit

und

ergibt wieder die wahre Aussage:

Die Berechnung der Relativgeschwindigkeit ist also mit der Lorentz-Transformation eine runde Sache, die aus der Sicht aller Bezugssysteme immer wieder denselben Charakter hat. Die Zwischenfrage ist hiermit also beantwortet

Meint
Euer Christoph

Willkommen zu einem weiteren Artikel der Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“.

Im vorletzten Artikel (siehe „Zurück an den Start“) haben wir die Lorentz-Transformation für Ereignisse angeschrieben (es gibt die LT übrigens auch für Kräfte, Impulse, elektromagnetische Feldgrößen, etc.).

Dabei haben wir akzeptiert, dass beim Wechsel von einem Bezugssystem in ein anderes sich nicht nur die Ortskoordinaten ändern, sondern auch die Zeitkoordinate.

Weiters haben wir, vorerst ohne Beweis, angekündigt, dass sich durch die Konstanz der Lichtgeschwindigkeit (also durch die LT) einige neue Relativitäten auftun.

So haben wir behauptet, dass Dinge wie „Länge“, „Gleichzeitigkeit“ und „Raum und Zeit“ ebenfalls keine absoluten (invarianten) Größen mehr sind sondern vielmehr vom Bewegungszustand des Beobachters (also von seiner Geschwindigkeit) abhängen.

Diesmal wollen wir diesen Behauptungen auf den Grund gehen. Am besten bedienen wir uns dazu der „Minkowski-Diagramme“.

Zur Wiederholung wollen wir vorerst die LT für Ereignisse hier nochmals anschreiben. Ein Ereignis wird hier durch ein Tupel (t,x) bzw. (t‘,x‘) beschrieben:

Rücktransformation vom „mitbewegten“ (gestrichenen) Bezugssystem ins „ruhende“:

Hintransformation vom „ruhenden“ (ungestrichenen) Bezugssystem ins „mitbewegte“:

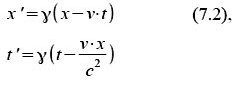
wobei folgende Abkürzung verwendet wird:

Was ist also ein Minkowski-Diagramm?

Wie wir bereits gesehen haben, ist die Lorentz-Transformation eine Linear-Transformation.

Das heißt, dass wir eine Ebene aus Raum- und Zeitkoordinaten (unsere zweidimensionale Raumzeit) durch zwei unterschiedliche Koordinatensysteme vermessen können, wobei die Koordinatensysteme sich so zueinander verhalten, wie sich ein quadratisches Raster zu einem parallelogrammartigen Raster verhält.

Nun kann man also ein Zeichenblatt nehmen, und mit diesem Zeichenblatt eine (t,x) – Ebene aufspannen. Sodann kann man in diese (t,x) – Ebene die Koordinatenachsen x=0 (t-Achse) und t=0 (x-Achse) einzeichnen.

Der besseren Übersichtlichkeit halber kann man die t-Achse mit der Lichtgeschwindigkeit c skalieren, um in beide Richtungen die Einheit Meter zu erhalten. Die Lichtgeschwindigkeit haben wir ja als fundamentale Naturkonstante akzeptiert und somit ist sie als konstanter Faktor geeignet.

Wenn man nun die Koordinatenachsen des gestrichenen („parallelogrammartigen“) Koordinatensystems einzeichnen möchte, ist es am besten, die beiden Ereignisse (ct’=0, x’=1) und (ct’=1, x’=0) der Lorentz-Rück-Transformation zu unterwerfen, und die sich daraus ergebenden Punkte (ct=γ.v/c,x=γ) und (ct=γ,x=γ.v/c) mit dem Ursprung durch je eine Gerade zu verbinden.

Das ergibt etwa folgendes Bild.

Die 45°-Linie ist die Weltlinie eines Lichtblitzes, der sich in Richtung der positiven x-Achse/x‘-Achse bewegt.

Dieser bewegt sich bezüglich beider Bezugssysteme mit derselben Geschwindigkeit, weshalb die x‘-Achse und die c.t‘-Achse „symmetrisch hereingeklappt werden“ (diese Symmetrie ist bei der Galilei-Transformation übrigens nicht gegeben).

Der Winkel α ergibt sich zu tg α=v/c, kann also nie größer als 45° bzw. kleiner als -45° werden (das würde dann also Bezugssystemen entsprechen, die sich mit einem „Vorwärts-Lichtblitz“ bzw. mit einem „Rückwärts-Lichtblitz“ mitbewegen).

Um nun die genannten Behauptungen zu untersuchen, wollen wir einen „ruhenden“ Stab im Minkowski-Diagramm interpretieren.

Sei der Stab definiert durch seinen Anfangspunkt P und seinen Endpunkt Q. Beide Punkte sollen relativ zum ungestrichenen Bezugssystem in Ruhe sein, der eine bei x=0, der andere bei x=L. Die Weltlinien der beiden Punkte ergeben sich also wie folgt:

Wie bereits beim letzten Mal geklärt (siehe „Manchmal sind offensichtliche Dinge gar nicht so offensichtlich“), bewegen sich beide Punkte mit der Geschwindigkeit (-v) relativ zum gestrichenen Bezugssystem.

Die nächste Frage ist die Frage nach der Länge des Stabes.

Aber wie misst man die Länge? Die einleuchtendste Definition scheint die zu sein, dass man „gleichzeitig“ die x-Koordinate (bzw. die x‘-Koordinate) des Punktes P und des Punktes Q misst, und dann die Differenz bildet.

Das heisst: um die Länge L im ungestrichenen Bezugssystem zu messen, setzen wir t=0 und messen x_P(t=0) und x_Q(t=0). Wie nicht anders zu erwarten, ergibt sich genau der Wert L.

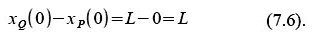
Übrigens müßten wir nicht unbedingt den Wert t=0 verwenden, sondern wir könnten jeden beliebigen „Messzeitpunkt“ t=t_m=const verwenden. Da die LT aber ohnedies eine Lineartransformation ist, würde das in unserem Fall keinerlei Informationsgewinn bedeuten.

Im folgenden Bild sind nun die beiden Weltlinien der Punkte P und Q in einem Minkowski-Diagramm dargestellt:

Da wir es nicht mehr mit einer absoluten Zeit zu tun haben, müssen wir für die Messung der Länge L‘ (im gestrichenen Bezugssystem) die Zeitkoordinate t‘ gleich 0 setzen (und nicht t). Die beiden strichlierten Linien zeigen uns, dass die Messungen von L und L‘ „an zwei unterschiedlichen Stäben durchgeführt werden“ (zumindest sind die beiden Ereignisse „Messung von x_Q“ und „Messung von x‘_Q“ nicht dieselben Ereignisse).

Aus der Sicht des ungestrichenen Bezugssystems werden also die gestrichenen Ortskoordinaten nicht „gleichzeitig“ gemessen, aus Sicht des gestrichenen Bezugssystems schon.

Das führt letzten Endes zu einer kompletten Überarbeitung des Begriffes der Gleichzeitigkeit.

Wie wir bereits beim letzten Mal berechnet hatten (siehe „Manchmal sind offensichtliche Dinge gar nicht so offensichtlich“), transformieren sich die Weltlinien der Punkte P und Q wie folgt in das gestrichene Bezugssystem:

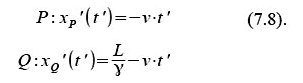
Die Länge L‘ ergibt sich also zu

Fazit:
Der „ruhende“ Stab ist also im „bewegten“ Bezugssystem kürzer, als im „ruhenden“ Bezugssystem (ich schreibe absichtlich er „ist“ im bewegten System kürzer, und nicht er „erscheint“ aus der Sicht des bewegten Beobachters kürzer).

Wie wir gesehen haben, entfällt in der speziellen Relativitätstheorie nicht nur der absolute Begriff der Länge sondern auch der absolute Begriff der Gleichzeitigkeit (da Gleichzeitigkeit ja vom Bezugssystem abhängt).

Was man aber absolut (unabhängig vom Bezugssystem) zu zwei Ereignissen und ihren Beziehungen immer noch sagen kann, ist eine Einteilung in einen der folgenden vier Fälle:

1. Man erreicht das eine Ereignis vom anderen mit Unterlichtgeschwindigkeit (die Verbindungsstrecke zwischen den beiden Ereignissen ist im Minkowski-Diagramm steiler als 45°)
2. Man erreicht das eine Ereignis vom anderen genau mit Lichtgeschwindigkeit (die Verbindungsstrecke zwischen den beiden Ereignissen ist im Minkowski-Diagramm also genau 45° steil)
3. Man erreicht das eine Ereignis vom anderen mit Überlichtgeschwindigkeit (die Verbindungsstrecke zwischen den beiden Ereignissen ist im Minkowski-Diagramm flacher als 45°)
4. Beide Ereignisse sind identisch

In der Relativitätstheorie nennt man diese Lagen der Ereignisse zueinander

1. eine „zeitartige“ Lage
2. eine „lichtartige“ Lage
3. eine „raumartige“ Lage

Philosophische Interpretation:

Meiner Meinung ist Fall 3 der philosophisch interessanteste. Letzten Endes bedeutet eine „raumartige“ Lage ja, dass die Reihenfolge der Ereignisse nicht absolut festgelegt ist, was man in einer philosophischen Sichtweise so interpretieren könnte, dass sie eben „quasi gleichzeitig“ stattfinden, weil eine eventuelle Kausalität zwischen den Ereignissen ja keine zeitliche Richtung mehr hat (oder man negiert die Möglichkeit einer absoluten Kausalität in diesem Fall).

Wenn also zwei Ereignisse z.B. einige Meter auseinander liegen (der „direkte Aktionsradius“ eines Menschen), dann haben wir keinen ZeitPUNKT, den wir als „Jetzt“ bezeichnen können, sondern bereits einen ZeitRAUM, den wir physikalisch als „Jetzt“ bezeichnen müssen, denn innerhalb dieses Zeitraumes gibt es keine klare Trennung zwischen „früher“ und „später“.

Da dieser Zeitraum <JETZT> allerdings weit unter dem Zeitraum liegt, den unser Gehirn als "Jetzt" erkennt, ergeben sich dadurch keine praktischen Probleme.

Bei großen räumlichen Abständen wird dieser Effekt deutlicher. Z.B. macht die Frage "Was passiert im Andromedanebel <JETZT>" aus Sicht der Relativitätstheorie keinen großen Sinn.

Meint
Euer Christoph