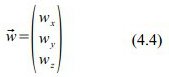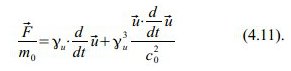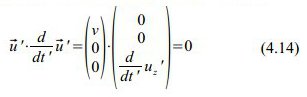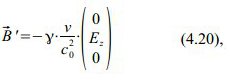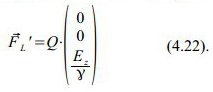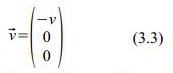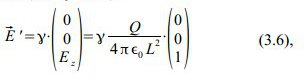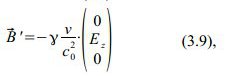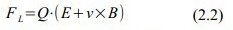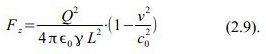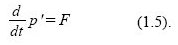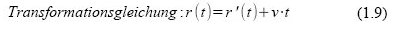In der Serie „ein kleiner Programmierer versucht, die Relativitätstheorie zu verstehen“ sind bisher folgende Beiträge erschienen:
- Hat SIMUL-RR etwas mit der Relativitätstheorie zu tun?
- Matter matters
- Das gute alte Relativitätsprinzip
- Widerspruch oder bloß eine Unschönheit?
- Aus Absolutheit folgt Relativität
- Alles geht sich sehr schön aus, oder?
Beim letzten Mal („Alles geht sich sehr schön aus, oder?“) haben wir mit Hilfe der LT das elektromagnetische Feld berechnet, mit dem eine Punktladung eine andere Punktladung beeinflußt, wenn beide parallel zueinander mit der Geschwindigkeit v durch den leeren Raum fliegen.
(1) Diesmal wollen wir das Modell ein wenig abändern.
Wir gehen wieder davon aus, dass die Punktladung K1 seit unendlich langer Zeit fest im Ursprung des ungestrichenen Bezugssystems verankert sei, die Punktladung K2 nimmt auch wieder in z-Richtung den Abstand L ein.
Diesmal wollen wir aber davon ausgehen, dass die Kugel K2 eine Masse m0 habe und sich durch das elektrische Feld in z-Richtung bewegen wird. Sie wird durch die Coulomb-Kraft eine Beschleunigung in z-Richtung erfahren.
Auch diesmal gehen wir von der Gültigkeit der Relativitätstheorie geradewegs aus und machen einfach ein Rechenbeispiel durch.

In der Relativitätstheorie kann man nicht mehr von „Gleichzeitigkeit“ sprechen, da sich der Zeitparameter t bei der Transformation ins gestrichene Bezugssystem ebenfalls transformiert. Dabei ist sowohl der Ort r‘ von r und t abhängig als auch der Parameter t‘ ist von r und t abhängig (r=(x,y,z) sei der ungestrichene Ortsvektor, r’=(x‘,y‘,z‘) sei der gestrichene Ortsvektor).
Da also bei der Lorentz-Transformation die Zeit mittransformiert wird, spricht man letzten Endes von einem vier-dimensionalen Vektor (einem „Vierervektor“), welcher die „Raumzeit“ darstellt.
Wir können also nicht mehr von einem „Startzeitpunkt“ t=0 sprechen, an dem wir die Kugel K2 „loslassen“, sondern wir müssen von einem „Startereignis“sprechen (t=0, x=0, y=0, z=L). Dieses „Ereignis“ können wir dann in ein anderes Bezugssystem transformieren.
Wir wollen wieder ein gestrichenes Bezugssystem festlegen, welches sich in negativer x-Richtung mit der Geschwindigkeit v bewegt,

sodass sich die Kugeln (anfangs) in positiver x‘-Richtung relativ zu diesem gestrichenen Bezugssystem mit der Geschwindigkeit v bewegen.
(2) Wir beschreiben nun die Bewegung der Kugel K2 durch ihre Geschwindigkeit u.
Im ungestrichenen Bezugssystem ist das also

Im Gegensatz zur Galilei-Transformation, wo Geschwindigkeiten einfach vektoriell addiert oder subtrahiert werden, ist die Formel für die Transformation von Geschwindigkeiten mit der LT ein wenig komplizierter.
Wieder gegoogelt, hier die Transformation einer allgemeinen Geschwindigkeit w vom ungestrichenen System ins gestrichene
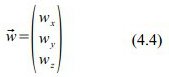
wird zu
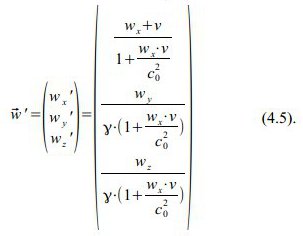
Auf unsere konkrete Geschwindigkeit u angewendet, bedeutet das im gestrichenen Bezugssystem

wobei γ wieder der Lorentz-Faktor ist, der sich aus der Relativgeschwindigkeit der beiden Bezugssysteme ergibt:

Wir haben aufgrund der Geometrie unseres Beispieles also nur eine einzige Variable – uz – durch die wir den Bewegungszustand der Kugel K2 ausdrücken können, v ist ja konstant.
(3) Jetzt wollen wir die Bewegungsgleichung anschreiben.
Bei der Bewegungsgleichung ergibt sich durch die Relativitätstheorie eine Änderung, da die Masse nicht mehr konstant ist, sondern von der Geschwindigkeit u der Kugel K2 abhängt:

Diese Gleichung gilt auch im gestrichenen Bezugssystem, bloß muss man dort m durch m‘ ersetzen und u durch u‘. Wenn u gleich Null ist (im sogenannten Ruhesystem), dann ist der Faktor γu gleich 1 und die Masse ist dann gleich der Ruhemasse m0.
Die Kugel hat also in jedem Bezugssystem eine andere Masse (da ja die Geschwindigkeit in jedem Bezugssystem eine andere ist), und demzufolge wird die Bewegungsgleichung signifikant komplizierter gegenüber der klassischen Mechanik.

differenziert nach der Produktregel,

und dann Gleichung (4.8) eingesetzt
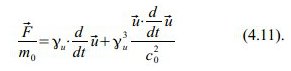
(4) Doch wir wollen die Sache ein wenig vereinfachen. Uns interessiert ja nur das Startereignis.
Deshalb vereinfacht sich die Bewegungsgleichung wie folgt.
Im ungestrichenen Bezugssystem gilt zur Raumzeit des Startereignisses

und γu=1, weshalb sich die Bewegungsgleichung vereinfacht zu

Im gestrichenen Bezugssystem gilt zur Raumzeit des Startereignisses uz‚=0, also
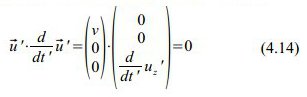
und γu=γ, weshalb sich die Bewegungsgleichung vereinfacht zu

(5) Die Kraft, die auf die Kugel K2 wirkt, ist die Lorentz-Kraft FL.
Wir wissen bereits vom letzten Mal, dass E-Feld und B-Feld relative Größen sind, denn sie hängen vom Bewegungszustand des Beobachters ab (das galt übrigens auch schon in der vor-relativistischen Elektrodynamik, da das Magnetfeld und die Lorentzkraft ja auch etwas mit der (Relativ-)Bewegung von Ladungsträgern zu tun haben).
Jetzt wird sich zeigen, dass auch der Wert einer Kraft F vom Bewegungszustand des Beobachters abhängt.
Letzten Endes hat ja genau diese Tatsache, dass aus der Absolutheit der Lichtgeschwindigkeit die Relativität so vieler physikalischer Größen folgt, dazu geführt, dass Einsteins Aufsatz – der ja ursprünglich lapidar „Von der Elektrodynamik bewegter Körper“ geheissen hatte – als „Relativitätstheorie“ in die Geschichte eingegangen ist.
Im ungestrichenen Bezugssystem ergibt sich die Lorentz-Kraft also aus dem elektrischen Feld:

Das Q in dieser Formel ist die Ladung der Kugel K2.
Wir wissen noch vom letzten Mal, dass der Wert Ez von der Ladung Q der Kugel K1 und vom Abstand L abhängt (wenn uns nicht nur das Startereignis interessieren würde, müßten wir statt L ganz allgemein die Koordinate z der Kugel K2 einsetzen).
Im ungestrichenen Bezugssystem bekommen wir also über die Bewegungsgleichung eine Querbeschleunigung

Die Lorentz-Kraft hat im gestrichenen Bezugssystem den Wert

Wenn man hier die gestrichenen Feldstärken vom letzten Mal hernimmt (gültig für die Raumzeit des Startereignisses),

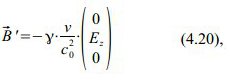
sie in die Definition der Lorentz-Kraft einsetzt,

und weiters berücksichtigt, dass uz‚ zur Raumzeit des Startereignisses gleich Null ist, so erhält man nach kurzer Rechnung die gestrichene Lorentz-Kraft, die wieder nur eine z‘-Komponente hat:
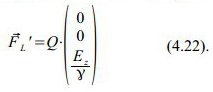
Im gestrichenen Bezugssystem bekommen wir über die Bewegungsgleichung also die Querbeschleunigung

Fazit:
Aus Gl. (4.16) und (4.22) sieht man also, dass die Kraft quer zur Bewegungsrichtung des Bezugssystems im gestrichenen Bezugssystem um den Faktor γ kleiner ist als die Kraft im ungestrichenen Bezugssystem.
Aus Gl. (4.17) und (4.23) sieht man, dass die Beschleunigung sogar um den Faktor γ2 kleiner wird.
Dies ist aber im Licht der LT einsichtig, denn die z-Koordinate wird durch die LT zwar gleich gelassen, aber es gibt eine Zeitdilatation.
Da sich die Querbeschleunigung durch zweimaliges Ableiten der Ortskoordinate z nach der Zeit ergibt, ist auch klar, dass der Faktor γ quadratisch in die Beschleunigung eingeht.
In die Kraft F geht der Faktor γ nur linear ein, da ja in der Gleichung F=m.a der Wert m ebenfalls von γ abhängt (m=m0.γ) und sich dieses γ gegen eines aus dem Wert von a kürzt (nach der LT).
Die Newton’sche Kraft F ist also auch eine relative Größe, da sie vom Bewegungszustand des Beobachters abhängt.
Auch Beschleunigungen sind in der Relativitätstheorie nichts Absolutes.
Meint
Euer Christoph



 Veröffentlicht von Yeti
Veröffentlicht von Yeti