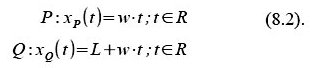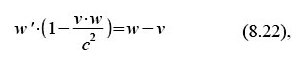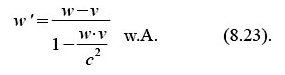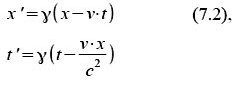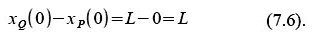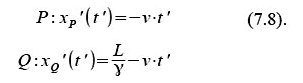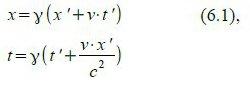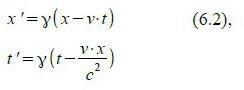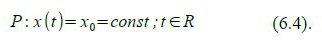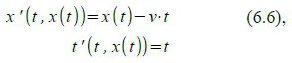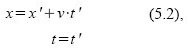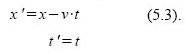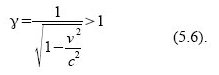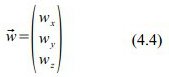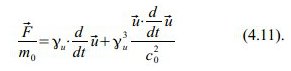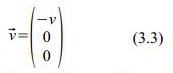Hier, im vorerst letzten Artikel der Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“, darf – zum krönenden Abschluss der speziellen RT – das sogenannte Zwillingsparadoxon nicht fehlen.
Wie die meisten von Euch wahrscheinlich schon wissen, geht es beim sogenannten Zwillingsparadoxon um ein gleichaltriges Brüderpaar, von denen der eine zuhause auf der Erde bleibt, während sich der andere in einem Raumschiff mit großer Geschwindigkeit auf den Weg macht, einen fernen Stern zu erforschen.
Danach kehrt er – wieder mit großer Geschwindigkeit – zurück.
Wenn der Forscher-Bruder zurückkehrt, wird sich herausstellen, dass er weniger gealtert ist als sein zuhause gebliebener Bruder (dass in seinem Bezugssystem weniger Zeit vergangen ist).
Und genau hier setzt der Vorwurf an, denn laut Lorentz-Transformation gilt der Faktor γ sowohl für die Hin- als auch für die Rücktransformation, und somit könnte jeder der beiden Brüder behaupten, die Uhr des anderen gehe langsamer.
Dieses scheinbare Paradoxon wurde bereits wenige Jahre nach Bekanntwerden aufgelöst, denn es wurde erkannt, dass eines der Systeme eben kein Inertialsystem ist, und man dadurch die Ergebnisse der Relativitätstheorie nicht so blauäugig anwenden kann.
Vielmehr muss man sich bewusst sein, dass durch die Umkehr am Endpunkt der Reise eine Umbewertung der Gleichzeitigkeit mit dem zuhausegebliebenen Bruder stattfindet, dass man also auch die Geschwindigkeitsänderungen (Krümmungen der Weltlinien) berücksichtigen muss.
Am besten, wir zeichnen die Weltlinie des Forscher-Bruders:
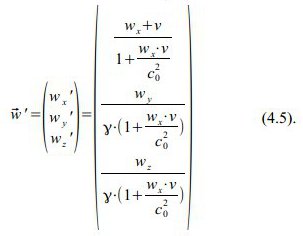
Hier haben wir gleich die zwei „bewegten“ Bezugssysteme mit eingezeichnet (eines für den Hinflug und eines für den Rückflug). Das erste nennen wir B'(t‘,x‘), es hat seinen Ursprung gemeinsam mit B(t,x), also beim Start des Forscher-Zwillings.
Das zweite (B“(t“,x“)) hat seinen Ursprung im Zusammentreffen der Zwillinge NACH der Reise, also bei t = 2.T (T ist die ungestrichene „Reisezeit für eine Richtung“).
v ist hier der Absolutbetrag der Reisegeschwindigkeit der Rakete.
Wie lauten nun die Lorentz-Transformationen für den Hinflug (wo wir B‘ verwenden wollen), und für den Rückflug (wo wir B“ verwenden wollen)?
Die Lorentz-Transformation für den Hinflug können wir direkt anschreiben, da wir diese Situation bereits kennen:
Um die Lorentz-Transformation für den Rückflug zu errechnen, definieren wir vorerst ein weiteres „ruhendes“ Bezugssystem (das denselben Ursprung hat wie B“):
Für dieses neue Bezugssystem können wir die Lorentz-Transformation direkt anschreiben, da es ja denselben Ursprung hat wie B“, und da wir wissen, dass sich B“ relativ zu diesem mit der Geschwindigkeit (-v) bewegt.
Wenn wir nun wieder vom „Dach“-Bezugssystem ins ursprüngliche „ruhende“ zurückrechnen, erhalten wir die Lorentz-Transformation für den Rückflug:
Doch nun zur Interpretation:
Was die Länge der Flugstrecke und die Dauer des Fluges betrifft, ist alles noch relativ einfach zu interpretieren.
Da sich der Forscher-Bruder mit der Geschwindigkeit v bewegt, verkürzt sich der Weg für ihn durch die relativistische Längenkontraktion auf die Länge
Da er selbst seine Relativgeschwindigkeit zum Weltall ebenfalls mit dem Wert v bewertet, vergeht während des Fluges in seinem Cockpit die Zeit
Wir sehen also
- „während“ des Fluges ist der Forscher-Bruder nur um die Zeit T’=T/γ gealtert
- „während“ des Fluges ist der Erden-Bruder um die Zeit T gealtert (also mehr)
Die Zeitangabe „während“ bezieht sich hier auf die Sichtweise des Erden-Bruders.
Aber wie alt ist der Erden-Bruder „aus Sicht des Forscher-Bruders“? Dieser kann doch genauso gut behaupten, dass sich die Erde relativ zu ihm bewegt und somit dort die Zeit langsamer verstreicht.
Da der Forscher-Bruder „exakt zum Zeitpunkt der Ankunft und Umkehr“ sich nicht in einem Inertialsystem befindet, sondern in einem beschleunigten System, und man somit nicht mehr die spezielle Relativitätstheorie anwenden kann, können wir uns nur folgende Fragen stellen (aus der Sicht des Forscher-Bruders).
- „Kurz vor meiner Ankunft“ am Ziel: „Wie alt ist mein Bruder auf der Erde <Jetzt>“?
- „Kurz nach meinem Abflug“ vom Ziel: „Wie alt ist mein Bruder auf der Erde <Jetzt>“?
Kurz vor der Ankunft gilt die Transformation für den Hinflug, kurz nach dem Abflug gilt die Transformation für den Rückflug.
Kurz vor der Ankunft (aus Sicht des Forscher-Bruders) befindet sich der Erden-Bruder am Ereignis t’=T‘, x=0 (er befindet sich immer bei x=0, und die Gerade t’=T‘ ist unser „Messzeitpunkt“).
Um aus diesen Werten das Alter zu berechnen, nennen wir es T1, benötigen wir die Transformation für den Hinflug:
Die Werte t‘ und x eingesetzt, kann man T1 in Abhängigkeit von T‘ zurückrechnen. Zuerst die bekannten Werte von t‘ und x eingesetzt
sodann die zweite Gleichung in die erste eingesetzt
und nach T1 aufgelöst
also
und endgültig
Der Erden-Bruder ist also „während“ des Fluges nur um die Zeit T1=T’/γ=T/γ2 gealtert.
Die Zeitangabe „während“ bezieht sich hier auf die Sichtweise des Forscher-Bruders.
Ähnliche Verhältnisse ergeben sich für den Zeitpunkt knapp „nach dem Abflug“, es ist aber anschaulicher, sich das im Minkowsi-Diagramm anzusehen, anstatt es „hardcore“ durchzurechnen:
Das Diagramm in Abbildung (9.17) macht deutlich, dass aus Sicht des Erden-Bruders das Abbrems- und Beschleunigungsmanöver tatsächlich „während“ eines (unendlich) kleinen Zeitraumes rund um die Zeitkoordinate t=T durchgeführt wird.
Aus Sicht des Forscher-Bruders wird die Gleichzeitigkeit aber anders bewertet, deshalb ist für ihn(!) bis zum Beginn des Bremsmanövers auf der Erde tatsächlich erst die Zeit T1 vergangen (T1=T/γ2), wie wir eine Seite weiter oben berechnet haben (Schnittpunkt der Geraden t’=T‘ mit der Geraden x=0).
Für den Forscher-Bruder macht die Zeit auf der Erde „während“ des Abbrems- und Beschleunigungsmanövers tatsächlich einen Sprung, nämlich von t=T1 zu t=2T-T1.
Wir sehen, dass das Zwillingsparadoxon kein Paradoxon ist, sondern lediglich dadurch zustande kommt, dass wir fehlerhafte Annahmen über die Bedeutung von Gleichzeitigkeiten treffen (die Idee einer absoluten Zeit sitzt offenbar tief in uns drinnen).
Zu sagen „während des Fluges“ geschieht dies oder jenes, kann keine absolute Aussage sein, da ja die Bedeutung von „während des Fluges“ vom Bewegungszustand des Beobachters abhängt.
Beobachter mit unterschiedlichem Bewegungszustand haben kein „gemeinsames <Jetzt>“.
Warum die Zeit auf der Erde einen Sprung „während“ des Brems-/Beschleunigungsmanövers des Forscher-Bruders durchmacht, liegt wahrscheinlich an dessen Beschleunigung.
Meiner bescheidenen Meinung nach müssen wir uns zur Klärung dieser Fragen aber mit der allgemeinen Relativitätstheorie (ART) beschäftigen, bisher hatten wir uns ja auf die spezielle Relativitätstheorie (SRT) beschränkt.
Jetzt mal eine schöne Karwoche an alle
meint
Euer Christoph

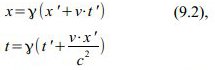
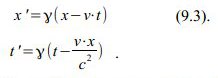






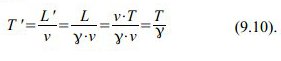










 Veröffentlicht von Yeti
Veröffentlicht von Yeti