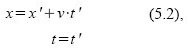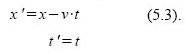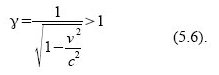Willkommen zu einem neuen Artikel in der Serie „Ein kleiner Programmierer versucht die Relativitätstheorie zu verstehen“.
Beim letzten Mal (siehe Zurück an den Start) haben wir intuitiv die sogenannte Galilei-Transformation hergeleitet, in der man zur gestrichenen Ortskoordinate das Korrekturglied v.t addiert, um zur ungestrichenen Ortskoordinate zu gelangen.
Dabei ist ohne weiteres einsichtig, dass v die Relativgeschwindigkeit der beiden Koordinatensysteme ist und t die (absolute) Zeit.
Dann haben wir die LT (Lorentz-Transformation) für eindimensionale Probleme angeschrieben. In diesem Formelwerk kommt – neben der Lichtgeschwindigkeit c – auch wieder der Buchstabe v zum Einsatz.
Aber was ist in diesen Gleichungen die Bedeutung von v?
Zur Wiederholung wollen wir die LT hier nochmals anschreiben:
Rücktransformation vom „mitbewegten“ Bezugssystem ins „ruhende“:
Hintransformation vom „ruhenden“ Bezugssystem ins „mitbewegte“:
wobei folgende Abkürzung verwendet wird:
Ist hier v also wirklich die Geschwindigkeit des gestrichenen Bezugssystems, gemessen im ungestrichenen Bezugssystem?
Und ist (-v) die Geschwindigkeit des ungestrichenen Bezugssystems, gemessen im gestrichenen?
Um diese Fragen zu klären, müssen wir erst einmal festlegen, was wir mit dem Begriff „Geschwindigkeit eines Bezugssystems“ überhaupt meinen.
Am anschaulichsten ist wohl folgende Definition: Ein Bezugssystem B‘ bewegt sich genau dann mit der Geschwindigkeit v relativ zum Bezugssystem B, wenn für jeden Punkt P, der in B‘ ruht (dort also die Geschwindigkeit 0 hat), in B die Geschwindigkeit v gemessen wird.
Ein Punkt P ruhe also im ungestrichenen Bezugssystem.
Wir beschreiben ihn durch seine Weltlinie. Die Weltlinie ist die Menge aller Ereignisse, die der Punkt passiert (bzw. die den Punkt erst definieren). Ein Ereignis wird durch seine Orts- und Zeitkoordinaten beschrieben. Im ungestrichenen Bezugssystem beschreiben wir also den „ruhenden“ Punkt durch seine Weltlinie:
Seine Geschwindigkeit ist dort
Wie transformiert sich nun diese Weltlinie x(t) in das andere Bezugssystem, wo wir sie als Funktion x'(t‘) beschreiben wollen?
Als kleine Vorübung wollen wir diese Weltlinie der Galilei-Transformation unterwerfen.
Wir setzen also die Funktion x(t) in die Transformationsgleichungen ein:
also
Zuerst die zweite Gleichung nach t auflösen (was trivial ist), und dann t(t‘) in die erste Gleichung einsetzen, daraus folgt:
Somit hat der Punkt, der im ungestrichenen Bezugssystem ruht, im gestrichenen Bezugssystem die Geschwindigkeit
Der „ruhende“ Punkt bewegt sich also relativ zum „bewegten“ Bezugssystem mit der Geschwindigkeit (-v), was nicht weiter verwundert, da sich das Bezugssystem selbst ja mit der Geschwindigkeit (+v) relativ zum „ruhenden“ Bezugssystem bewegt.
Man beachte auch den sorgfältigen Umgang mit den Variablen t und t‘. In der Newton’schen Mechanik sind wir gewohnt, t=t‘ zu setzen, da wir von einer absoluten Zeit ausgehen. Im folgenden werden wir sehen, dass das bei Einstein nicht mehr selbstverständlich ist.
Doch nun zur Lorentz-Transformation.
Wir gehen wieder von folgender Weltlinie aus
setzen sie diesmal aber in die LT ein. Da wir aus dem vorigen Beispiel schon wissen, dass wir die Rücktransformation für t – also t(t‘,x‘) – benötigen, um sie in die Funktion x(t) einzusetzen, verwenden wir folgende beiden Transformationsformeln (teilweise von der Hin-, teilweise von der Rücktransformation):
Wenn wir nun die Weltlinie des Punktes P – also x(t) – in die erste Gleichung einsetzen, können wir die Weltlinie in das andere Bezugssystem transformieren:
Die zweite Gleichung in die erste eingesetzt, und dann nach x‘ aufgelöst, ergibt in weiterer Folge x'(t‘).
Zuerst eingesetzt
und dann alle Summanden mit x‘ auf die linke Seite gebracht
vereinfacht mit
zu
und weiter
Wir sehen also, dass der Punkt, der im „ruhenden“ Bezugssystem am Wert x=x0 stillsteht, sich relativ zum „bewegten“ Bezugssystem tatsächlich mit der Geschwindigkeit (-v) bewegt (das ist noch kein Unterschied zur Galilei-Transformation), und dass der Punkt zur Zeit t’=0 bei x’=x0/γ liegt (im Gegensatz zu x0 bei der Galilei-Transformation).
Der zweite Effekt ist ein Hinweis auf die relativistische Längenkontraktion, die wir nächstes Mal näher beleuchten wollen.
Lg
Euer Christoph
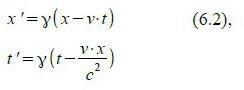

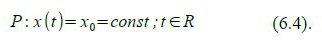

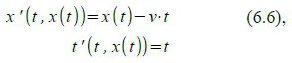














 Veröffentlicht von Yeti
Veröffentlicht von Yeti