Wie in meinem letzten Artikel zur Relativitätstheorie angekündigt (siehe „Das gute alte Relativitätsprinzip“), möchte ich diesmal konkret ein Rechenbeispiel durchmachen, das einen Widerspruch oder zumindest eine Unschönheit in der klassischen Betrachtungsweise der Elektrodynamik aufzeigt.
Im letzten Beitrag war die Rede von klassischer Mechanik und von der sogenannten Galilei-Invarianz derselben.
Diesmal wollen wir uns von der Mechanik auf die Elektrodynamik verlegen und versuchen, anhand eines Rechenbeispiels zu zeigen, warum die klassische Elektrodynamik (also die ohne Relativitätstheorie) eben NICHT galilei-invariant ist.
Das hatte um die Jahrhundertwende ja dazu geführt, dass man vorerst meinte, es muss eben DOCH ein ausgezeichnetes Inertialsystem geben und dieses sei jenes, welches sich relativ zum sogenannten Äther nicht bewege.
Schlußendlich führte aber kein Weg an der Relativitätstheorie vorbei.
Da mich Pink Panther darauf hingewiesen hat, dass das Modell der beiden parallel fliegenden Elektronen nicht realistisch ist (denn wie soll man diese auf parallelen Flugbahnen halten, wenn eben Kräfte normal zur Bewegungsrichtung wirken), möchte ich hier gerne das folgende leicht modifizierte Modell durchrechnen.
Modell: Zwei kleine, metallische, geladene Kugeln seien durch einen Isolatorstab starr miteinander verbunden und bewegen sich mit konstanter Geschwindigkeit v durch den ansonsten leeren Raum. Das sich ergebende hantelförmige Gebilde sei in folgender Abbildung erklärt:
Die Kugeln K1 und K2 seien – jede für sich – mit der Ladung Q geladen. Ihr Radius sei sehr klein gegen die Länge L des Isolatorstabes, sodaß man sie beim Lösen der Maxwell-Gleichungen als Punkt-Ladungen betrachten kann.
Der starre Isolatorstab sei sehr dünn – sodass man seine Anwesenheit beim Lösen der Maxwell-Gleichungen vernachlässigen kann.
Die Kugel K1 bewege sich entlang der x-Achse in Richtung positiver Werte.
Die Kugel K2 sei in Richtung der positiven z-Achse um den Wert L von der Kugel K1 entfernt.
Wenn wir es nun mit einer Anordnung von Ladungen (Ladungsträgern) zu tun haben, dann gibt es laut klassischer Elektrodynamik folgende Effekte.
- Jede Ladung verursacht ein elektrisches Feld E
- Jede bewegte Ladung verursacht ein magnetisches Feld B
- auf jede Punktladung wirkt im elektromagnetischen Feld die Lorentz-Kraft im weiteren Sinne FL=Q.(E+v×B). Dabei ist Q der Wert der Ladung und v ihre Geschwindigkeit.
Die ersten beiden Punkte werden in den Maxwell-Gleichungen beschrieben (Näheres dazu findet man zum Beispiel im Lehrbuch „Das elektromagnetische Feld“ von H.Hofmann – Achtung, mathematisch anspruchsvoll).
Der dritte Punkt ist eigentlich genau genommen erst die Definition des elektromagnetischen Feldes, denn dieses ist ja genau dadurch definiert, dass auf einen Ladungsträger im elektromagnetischen Feld die Kraft FL wirkt.
Nun wollen wir also den Wert der beiden Felder B und E errechnen, durch die die Punktladung K1 die Punktladung K2 beeinflußt. Hierzu muss man nur den Anteil des Feldes errechnen, den die Ladung K1 verursacht (man muss also die Maxwell-Gleichungen für K1 lösen).
Wir wollen das für den allgemeinen Fall einer Geschwindigkeit v tun (wenn sich die Ladungen also gegen das Inertialsystem bewegen, in dem der Beobachter sitzt).
Für den Spezialfall des mitbewegten Systems brauchen wir dann nur die Geschwindigkeit v=0 zu setzen.
Wie wir aus der Abbildung ersehen, verursacht die Kugel K1 im Wesentlichen ein radiales elektrisches Feld E und, da sie sich bewegt, ein tangentiales magnetisches Feld B (der Ladungstransport wegen der Bewegung von Kugel K1 bewirkt einen Wirbel im magnetischen Feld, weswegen dieses zylinderartig um die Flugbahn von K1 angeordnet ist).
Wegen der beiden Felder wirkt auf die Kugel K2 die Lorentz-Kraft FL, wobei v hier die Geschwindigkeit der Kugel K2 ist:
Die Pfeile von E und B weisen im Bild nur dann in die richtige Richtung, wenn Q größer als Null ist (wenn man den metallischen Kugeln also Elektronengas entzogen hat), ansonsten muß man ihre Richtung invertieren. In diesem Fall ist der Wert Q in der Lorentz-Kraft allerdings ebenfalls negativ, weshalb die Kräfte immer noch in dieselbe Richtung weisen, elektrische Kraft nach aussen, magnetische Kraft nach innen.
Aus den Maxwell-Gleichungen folgt nun konkret (für Interessierte und aus Gründen der Dokumentation ist die Berechnung der folgenden Gleichungen (2.3) und (2.4) hier hinterlegt), dass am Ort der Kugel K2 folgende Felder wirken, die von Kugel K1 herrühren:
mit der Abkürzung
Achtung: Die Gleichungen (2.3) und (2.4) unterliegen keiner Qualitätskontrolle (die Berechnung wurde nicht gegengelesen), sie können also Rechenfehler enthalten. Ich habe auf die Schnelle im Internet keine Quelle gefunden, um die Ergebnisse dieser Rechnung zu kontrollieren, das Rechenbeispiel ist aber dokumentiert und
nachvollziehbar (s.o.).
Sei es wie es sei, die Ergebnisse bestätigen die Aussagen, die auf Wikipedia getätigt werden, dass sich nämlich die Gesamtkraft in z–Richtung (also quer zur Flugrichtung, in Richtung des verbindenden Isolatorstabes), aus folgenden Komponenten zusammensetzt:
also
Hier sehen wir bereits, dass die Kraft des elektrischen Feldes in z-Richtung wirkt (also nach aussen), und die Kraft des magnetischen Feldes in (-z)-Richtung (also nach innen).
Um nun die beiden Anteile nach ihrer Größe zu vergleichen, benützen wir den allseits beliebten Zusammenhang zwischen der Dielektrizitätskonstante des leeren Raumes, der Permeabilität des leeren Raumes und der Lichtgeschwindigkeit im leeren Raum,
und formen Gleichung (2.7) ein wenig um:
Solange die Geschwindigkeit v also sehr klein ist gegen die Lichtgeschwindigkeit, ist die elektrische Kraft auch sehr viel größer als die magnetische und erst bei v=c0 tritt Gleichstand der beiden Kräfte ein (sodass in Summe keine Kraft auf die Kugel K2 wirken würde).
Allerdings, und das ist jetzt der Beweis dafür, dass die Elektrodynamik eben nicht galilei-invariant ist, ändert sich die Gesamtkraft mit dem Bewegungszustand des Beobachters (den wir ebenfalls durch die Geschwindigkeit v ausdrücken können: v=0 heißt „mitbewegter Beobachter“).
Denn so sehr man es akzeptieren könnte, dass die Aufteilung des elektromagnetischen Feldes in E-Feld und B-Feld eben vom Bewegungszustand des Beobachters abhängt (da die Gesamtkraft auf die Ladung eben nur als Kombination von Q.E und Q.v×B gemessen werden kann (siehe Gleichung (2.2))), so wenig kann man aus klassischer Sicht tolerieren, dass sich die Gesamtkraft als abhängig vom Bewegungszustand des Beobachters erweist.
Das sieht man, wenn man γ in Gleichung (2.9) als Funktion von v auffasst:
Der Faktor γ ist nur für kleine Geschwindigkeiten gleich 1, wird für größere Geschwindigkeiten immer größer und strebt für v −> c0 dann gegen Unendlich.
Interessant ist auch, dass sich in Gleichung (2.4) eine nicht verschwindende x-Komponente der elektrischen Feldstärke ergibt, was die Möglichkeiten eines Perpetuum Mobile eröffnen würde.
Man sieht also, dass bei Annahme der Gültigkeit der Galilei-Transformation die – an sich sehr gut belegten – Maxwellgleichungen zu Widersprüchen führen.
Dem wurde dann Abhilfe geschaffen, indem man die Lorentz-Transformation einführte, mit der wir uns beim nächsten Mal beschäftigen wollen.
Hinweise auf Rechenfehler willkommen.
meint
Euer Christoph

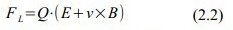






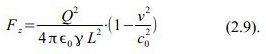




 Veröffentlicht von Yeti
Veröffentlicht von Yeti