Wie versprochen, werde ich mich in diesem und den nächsten Artikeln ein wenig mit der Relativitätstheorie beschäftigen.
Na gut, die spezielle Relativitätstheorie hat jetzt ja auch schon ihre guten 100 Jahre auf dem Buckel, trotzdem war schon damals das sogenannte „Relativitätsprinzip“ eigentlich ein alter Hut.
Galileo Galilei hat es ja schon formuliert, dass die Formulierung der Naturgesetze für alle Inertialsysteme gleich sein muss. Damit gibt es unter allen Inertialsystemen kein einziges, welches in irgendeiner Weise ausgezeichnet ist, da die physikalischen Gesetze ja überall in gleicher Weise gelten.
Und für die klassische Mechanik ist das auch wunderbar gültig. Man sagt, diese ist galilei-invariant.
Wir werden hingegen sehen, dass die Gleichungen der Elektrodynamik nicht galilei-invariant sind. Dies hat letzten Endes dazu geführt, dass man in der speziellen Relativitätstheorie die Galilei-Transformation ersetzt hat durch die Lorentz-Transformation. An die Stelle der Galilei-Invarianz ist dann die Lorentz-Invarianz getreten.
Aber was ist das überhaupt, ein Inertialsystem?
Man kann es so sagen: das ist, wenn man bei einem Raumschiff den Antrieb ausschaltet.
Dann befindet man sich innerhalb dieses Raumschiffs in der „absoluten Schwerelosigkeit“, also in der „relativen Ruhe“. Wie immer bei mir, hübsch flapsig formuliert das Ganze.
Nun könnte man innerhalb dieses Raumschiffs jedes beliebige Objekt durch seine Position beschreiben, also zum Beispiel einen Massenpunkt P:
r'(t) sei dabei die Position „relativ zum Raumschiff“ in Abhängigkeit von der Zeit, wir bezeichnen das Raumschiff als das „gestrichene Koordinatensystem“ (obwohl es vielleicht gar nicht gestrichen ist, sondern metallisch blank 🙂 ):
Wenn wir nun die Bewegungsgröße p‘ des Punktes ändern wollen, müssen wir eine Kraft auf den Punkt wirken lassen, das sagt uns die Newton’sche Bewegungsgleichung (allseits beliebt als „F=m.a“):
bzw.
bzw.
Wenn man hier die klassische Definition der Bewegungsgröße („Impuls gleich Masse mal Geschwindigkeit“) einsetzt und wenn man annimmt, dass die Masse des Massenpunktes konstant bleibt, also
also
dann erhält man die Rechenregel, nach der man den Weg des Massenpunktes im gestrichenen Koordinatensystem errechnen kann. Natürlich muss man zum Lösen dieser Differentialgleichung den Verlauf der Kraft F(t) kennen und die Anfangsbedingungen. Im folgenden Ausdruck sind die Variablen μ und τ sozusagen Laufvariablen für die Zeit t, die nur innerhalb des Integrals eine Bedeutung haben und deshalb benannt werden können, wie es beliebt:
Wenn wir nun wissen, dass sich das Raumschiff mit der Geschwindigkeit v relativ zu einem anderen Inertialsystem bewegt (nennen wir dieses das „ungestrichene Koordinatensystem“), dann können wir den Ortsvektor r'(t) – Ort des Massenpunktes relativ zum gestrichenen Koordinatensystem – in den Ortsvektor r(t) umrechnen – relativ zum ungestrichenen System.
Hierzu verwenden wir folgende Transformationsgleichung:
Wie aus dem Bild leicht einsichtig wird, muss man also zum gestrichenen Ortsvektor r'(t) den Wert v.t hinzufügen, um r(t) zu errechnen.
Wir gehen hier davon aus, dass die beiden Koordinatensysteme nicht gegeneinander verdreht sind, und dass sie zum Zeitpunkt t=0 identisch sind.
Um nun die Bewegungsgleichung in das ungestrichene Koordinatensystem zu transformieren, lösen wir die Transformationsgleichung nach r‘ auf (wir erhalten dadurch die Gleichung für die Rücktransformation) und setzen das erhaltene r‘ = r'(r,t) in die Bewegungsgleichung ein:
Dabei sehen wir, dass der Anteil v.t durch das zweimalige Differenzieren komplett entfällt:
also sieht die Bewegungsgleichung im ungestrichenen Koordinatensystem genauso aus, wie im gestrichenen:
Was nichts anderes ist als eine Folge der Tatsache, dass die klassische Mechanik eben galilei-invariant ist.
Um nun zu zeigen, dass die elektrodynamischen Gleichungen nicht galilei-invariant sind, gehen wir von einem einfachen Rechenbeispiel aus.
Vorausgeschickt: Die Elektodynamik beschäftigt sich mit der wechselseitigen Beeinflussung von Ladungsträgern. Wenn also ein Massenpunkt P gleichzeitig eine Ladung trägt, dann gibt es folgende Effekte:
- Jeder Ladungsträger verursacht ein elektrisches Feld E
- Jeder bewegte Ladungsträger verursacht ein magnetisches Feld B
- das elektrische Feld übt auf jeden Ladungsträger eine Kraft aus
- das magnetische Feld übt auf jeden bewegten Ladungsträger eine Kraft aus.
Wie man das elektromagnetische Feld berechnet, welches von einer – bewegten oder unbewegten – Anordnung von Ladungsträgern verursacht wird, ist in den Maxwell-Gleichungen beschrieben.
Dieses elektromagnetische Feld, beschrieben durch die Größen E(x,y,z,t) und B(x,y,z,t) beeinflußt einen Ladungsträger, der sich mit der Geschwindigkeit v bewegt, durch die sogenannte Lorentz-Kraft.
Der Wert q ist hierbei der Wert der Ladung, gemessen in Coulomb.
Man sieht, dass sich der magnetische Anteil der Lorentz-Kraft quer zur Bewegungsrichtung auswirkt (Kreuzprodukt).
Für unser Rechenbeispiel stellen wir uns zwei Elektronen vor, die sich in zwei parallelen Flugbahnen bewegen, und zwar beide mit der Geschwindigkeit v. Das erste Elektron nennen wir E1, das zweite nennen wir E2, beide haben die Ladung (-e).
Wenn wir nun im mitbewegten Koordinatensystem verharren, sind die beiden Elektronen bewegungslos, somit gibt es kein Magnetfeld und wir erhalten für die Lorentz-Kraft einen anderen Wert als im ruhenden Koordinatensystem.
Jedenfalls laut Wikipedia zeigt dieses Beispiel, dass die Gleichungen der Elektrodynamik eben NICHT galilei-invariant sind. Ob dem wirklich so ist, wollen wir nächstes mal untersuchen, wenn wir der zugehörigen Mathematik auf den Grund gehen.
Lg
Christoph




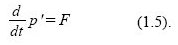



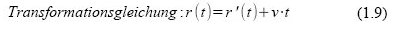


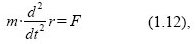






 Veröffentlicht von Yeti
Veröffentlicht von Yeti